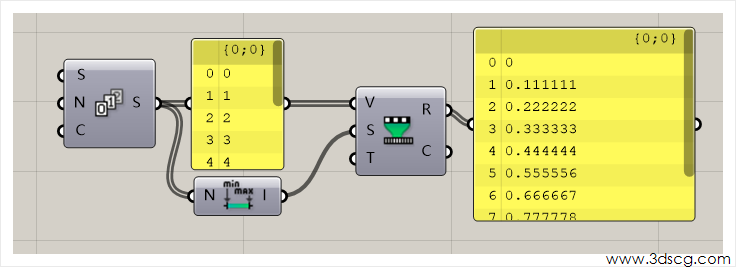
从这一节课开始后我们要开学习Grasshopper的数学了，Grasshopper给我们提供各式各样的数学工具，有了数学工具这个强大的武器，即使是数学不好的同学也能够利用数学设计建筑。
在数学里，区间通常是指这样的一类实数集合：如果x和y是两个在集合里的数，那么，任何x和y之间的数也属于该集合。例如，由符合0 ≤ x ≤ 1的实数所构成的集合，便是一个区间，它包含了0、1，还有0和1之间的全体实数。
Construct Domain：创建数字区间，比如创建一个10到20的数字区间
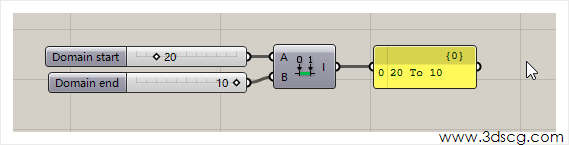
Deconstruct Domain：分解区间，分解区间后将会得到区间的两个极值，就是最大值最小值。
Bounds：从数据列表中获取最大值和最小值，然后输出数字区间。
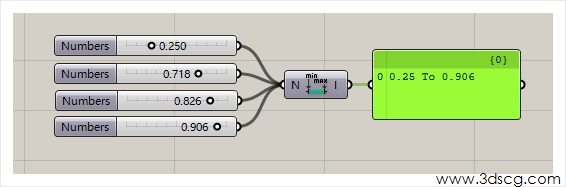
Consecutive Domains：划分区间，划分的方法有两种，默认情况下是这样划分的，请看下图
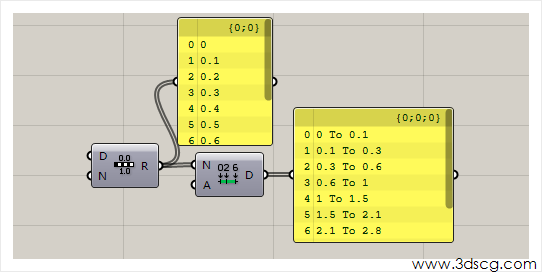
这个运算器的N输入一个等差数列（当然不是等差数列也可以的，等差数列是比较常见的用法），D端口输出划分后的区间集合
这个区间集合的规律是等差数列的0项和1项组成区间1，1项和3项组成区间2，3项和6项组成区间3，……以此类推。
| 开始项 | 结束项 | 输出区间 | |
| 0 | 1 | 组成 | 区间1 |
| 1 | 3 | 组成 | 区间2 |
| 3 | 6 | 组成 | 区间3 |
| 6 | 10 | 组成 | 区间4 |
| 10 | 15 | 组成 | 区间5 |
如果A端口输入FALSE
输出的区间则为下图所示：它会以输入列表的最大值作为结束端，输出等分的区间集合
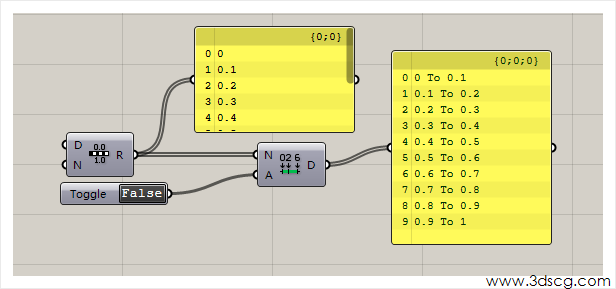
Divide Domain：等分区间，按照输入的等分数等分大区间，输出等分后的区间集合，下图是[5,8]的区间划分了6等分
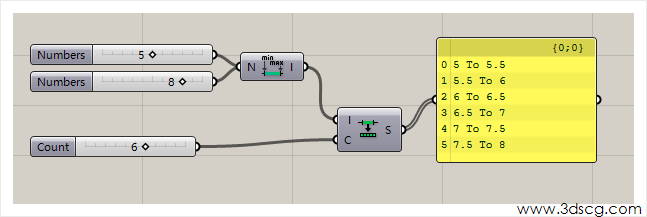
Find Domain：查询区间的序号，根据输入的数据就能查询包含这个数据的区间的序号，所谓序号（Index）就是Panel上最左边一列从0开始的编号
下图中输入的值为6.350，经过查询找出它属于编号为2的这个区间（6 to 6.5）
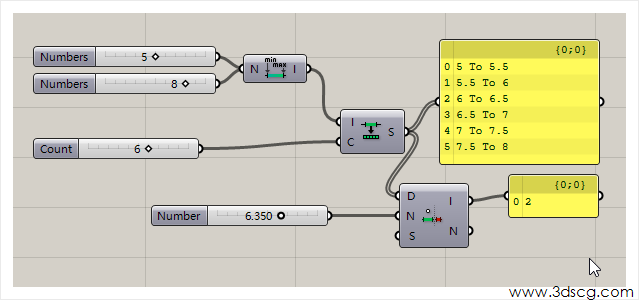
Includes：判断数值是否包含在指定的区间内，如果是输出True,如果不是则输出False。
下图中判断2和6.350这两个数是否在[5,8]这个区间，结果是False和Ture。
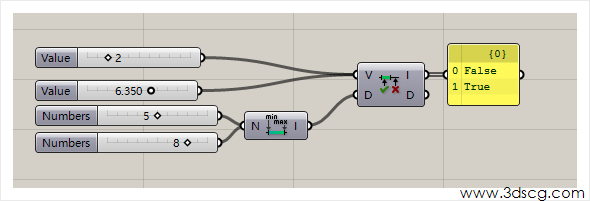
Remap Numbers：重映射区间，这个运算器在Grasshopper应用当中是很重要的，其作用就是改变原有区间的取值范围，比如[5,666]的区间的所有数字可以映射为[0,1]或其他的取值范围。
如下图输入的值是0 1 2 3 4 5 6 7 8 9这样的等差数列数字集合，经过Remap后输出的结果被限定在0到1之间，Remap 的T端口就是输入限定的区间大小，默认值为0 to 1
好的，我们今天课程就到这里，如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言，这样可以讨论关于Grasshopper的技术问题，我是LinkLi，下次课再见。