今天我们来讲解grasshopper向量的操作。向量在学习和使用grasshopper的时候也是占有比较重要的地位的。
Deconstruct Vector：解构向量
最终输出向量的xyz三个坐标。
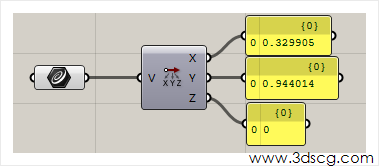
Vector XYZ：输入xyz三个坐标生成向量。
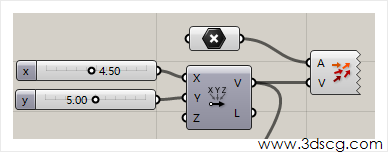
这几个是grasshopper默认的向量运算器。
Unit Vector：向量单位化，不管多大的向量，只要输入这个运算器之后，它都会变成0~1之间的单位
Unit X： 世界坐标的x方向。
Unit Y：世界坐标的y方向。
Unit Z：世界坐标的z方向。
Amplitude：给向量重新赋值。
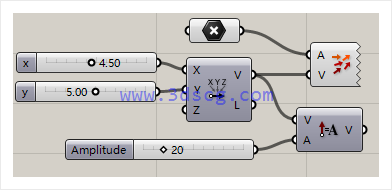
在修改向量大小的时候，通常会使用这样的一个计算器。
在下图中a端口输入一个新的值，会改变向量的大小。
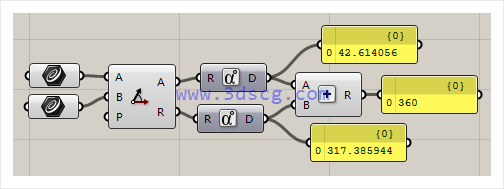
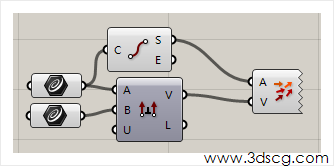
Angle：计算两个向量之间的角度。
A端口输出两个向量之间的夹角。
R端口输出两个向量的补角。
Cross Product：向量的叉乘
向量的叉乘，即求同时垂直两个向量的向量，即c垂直于a，同时c垂直于b（a与c的夹角为90°，b与c的夹角为90°）
在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示：
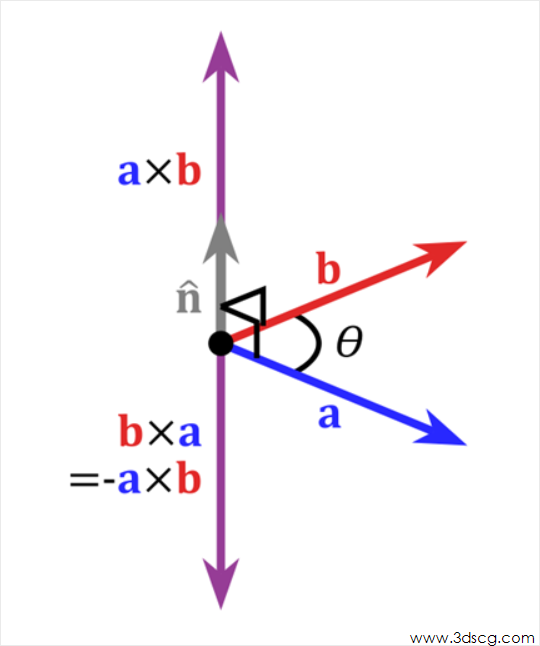
在二维空间中，叉乘还有另外一个几何意义就是：aXb等于由向量a和向量b构成的平行四边形的面积。
Dot Product：计算向量点积（内积）
向量的点乘,也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。
点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影
Reverse：翻转向量的方向。
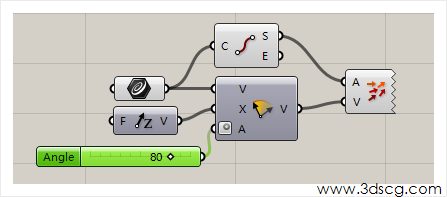
Rotate：旋转向量
X端口输入向量旋转的轴。
Vector 2Pt： 根据两个已知点生成一个向量。
Vector Length：输出出向量的长度。
好的，我们今天课程就到这里，如果有其他关于Grasshopper的其他问题也可以在本节课下面的留言窗口留言，这样可以讨论关于Grasshopper的技术问题，我是LinkLi，下次课再见。