斐波那契数列原理解析与Grasshopper插件应用

本文原文出自斐波那契数列插件的作者的文档，中文为谷歌翻译，翻译难免会出错，有问题可以下面评论区讨论

PhylloMachine 是一组脚本/用户对象，用于 Grasshopper 使用一些叶序的特性。基本思想是具有叶序比例的网格具有由两个描述的拓扑斐波那契数及其拓扑（面顶点索引、寄生螺旋、循环和拓扑邻居）由简单的数列描述，无需几何计算。由于这些，它可以参数化地建模植物器官，如树枝、树叶或花瓣，具有非常自然的效果。 PhylloMachine 仍在开发中，它是用 VisualBasic 编写的，并且是开源的。我鼓励那些有兴趣进一步开发这个插件的人与我联系，特别是如果他们有使用 L-Systems 的经验。

作者的邮箱: dga_3@hotmail.co

介绍

叶序是自然界中描述植物间空间分布的一类模式器官。每个物种都有自己的形式模式，可能是最大化的进化解决方案资源和成本最小化。 Phyllotaxis（来自古希腊语，phýllon“叶”和táxis“排列”）在植物学和生物数学作为茎上叶子的排列，可以优化叶子相对于其他叶子的位置，以最大限度地晒太阳，最大限度地减少干扰它们之间。有几种类型的叶序，但这里让我们只关注螺旋叶序，发散角137.5度。它是自然界中最常见的类型，并密切相关对于 phi 数，0,618 ^ 2 * 360 = 137.5 称为黄金角，正如我们将看到的还有斐波那契数列： 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144..

在坐标中，我们可以表示一个集合从中心旋转 137.5 度的点和在每次迭代时增加半径和角度。

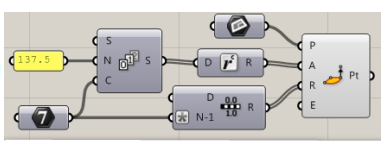
斐波那契数列原理解析与Grasshopper插件应用

视觉通过接近形成的螺旋形状点之间与斐波那契数列相连数并且是网状拓扑的基础千叶机。

斐波那契数列原理解析与Grasshopper插件应用

在曲线上应用这种点的分布，我们得到基本的网格点集合称为 PhylloPoints。在下图中，显示的是球体而不是点，以便于查看在两个方向形成的螺旋，顺时针和逆时针。这些螺旋以 Paraschies 的名义而闻名。

网状拓扑 – 寄生数

PhylloMachine使用phyllotaxis的一些属性将曲线包裹在四边形网格上，添加器官，如花瓣、叶子或树枝。 PhylloMachine 的所有组件都旨在使用四顶点面，因此不鼓励使用三角形网格。当网格由以下定义时被认为是 PhylloMesh：

可重新映射到圆柱坐标的点，
定义网格拓扑的寄生数。

Parastichy numbers 是斐波那契数列的一对数字 (a, b) – 连续祖先或后代。可以使用其他数字，例如其他类型的卢卡斯系列phyllotaxis，但在 PhylloMachine 中并非如此。这两个数字分别描述了顺时针和逆时针方向。在这种情况下，螺旋是指由以下公式形成的假想曲线在叶子、树枝或花瓣的循环之间连接某些植物器官。

在这张图片中，我们看到了寄生数的两种组合。上图显示 PN = (3, 5)，下图PN = (21, 34)。这些数字对于每种植物来说都是独一无二的，并且与每个周期的元素数量相关联，而一个周期是一整圈所有螺旋。一个循环的大小为 a + b，在上图 8 上，下图 55。越大每个周期的元素数，寄生数越大

此外，寄生数对应于最接近第一个点的索引列表的点。在下图中，从左到右，我们有：在一组 phyllopoints 中（用你可以在这里看到的定义制作），两个最接近的点索引 0 处的点是数字 3 和 5，它们对应于寄生数字。这些两个数字与 a) 点数，b) 半径 c) 曲线的长度有关。保持变量 b 和 c 不变并增加点数，会有一段时间当 PN 为 (5, 8) 时，如果我们继续 (8, 13)

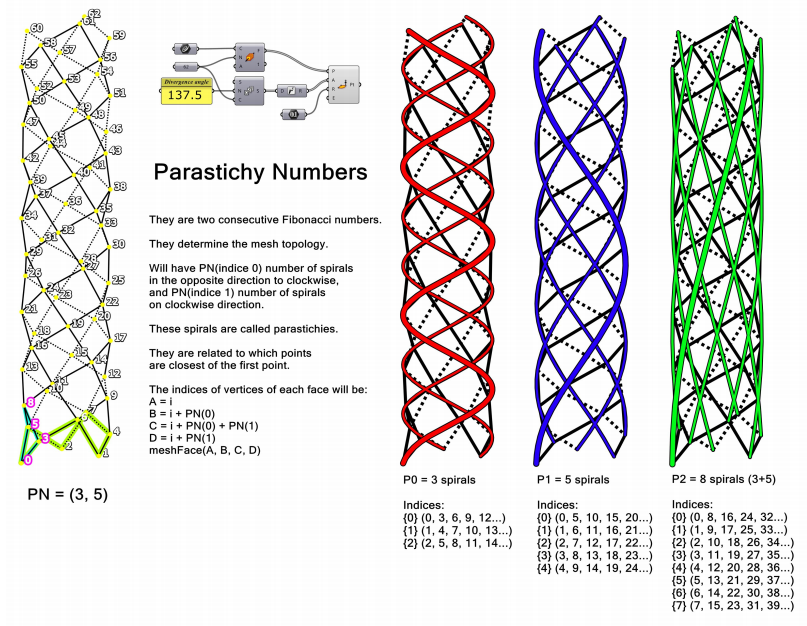
斐波那契数列原理解析与Grasshopper插件应用

位于寄生数 (3, 5) 上方的下一个点是 8（即 3 + 5）。因此我们可以说，要从 phyllopoints 形成 phyllomesh 的面，它认为：设 A、B、C 和 D 是每个点的迭代函数中每个顶点的索引（除了最后 a + b 个元素，在本例中为 3 + 5，即对于除最后 8 个之外的所有点），我们有：

A = 指数
B = 指数 + PN (a)
C = 指数 + PN (a) + PN (b)
D = 指数 + PN (b)

网格面（A、B、C、D）在我们的例子中 PN = (3, 5) 将是：

面 (0) = (0, 3, 8, 5)
面 (1) = (1, 4, 9, 6)
面 (2) = (2, 5, 10, 7

如果我们想翻转面的方向来反转法向量，一个简单的方法必须反转寄生数，即 PN = (b, a)。

在下图中，我们看到了如何根据上述解释管理点数每个面的顶点索引。 Merge 组件有一个包含四个点的列表（而不是四个索引如上）在每个分支内。那么包含少于 4 个的分支元素（只有这样 Construct Mesh 组件不会因缺少点而返回错误）是移除。

这是 PhylloMesh 的基本拓扑，但寄生数也决定了，没有进行几何计算、拓扑邻居、循环和螺旋寄生。

组件

我们有四组组件：

第一组包括所有组件 PhylloMeshes；
第二组对分支等器官起作用，叶子和花瓣；
第三组有修改的组件；
第四组包含实用程序。

PhylloBranch

包裹一条曲线以形成具有叶序图案的网格，并将一端焊接到网格面。

PhylloMachine

包裹曲线以形成具有叶序图案的网格的主要组件。也返回每个面的顶点索引，8个相邻索引，螺旋寄生索引
PN(a)、PN(b)和PN(a)+PN(b)，以及周期索引

PhylloSurface

通过圆柱重映射在表面上创建 PhylloMesh

PhylloMesh

使用 PhylloMesh 的裸边缘覆盖末端，形成具有叶序的网格

BezierCurve

从网格面快速创建四个点的贝塞尔曲线。它用于塑造树枝、花瓣和树叶的形状

Branch

挤出一个网格面，其中包含几个控制其大小的细分。它可用于创建分支、茎或种子。

Petal

从网格面和引导曲线创建花瓣或叶子

ExplodeMesh

将网格的面作为单个网格返回

MoveFac

移动和缩放网格面

OffsetMesh

根据距离或距离列表挤压网格以形成实体。

JoinMes

将多个网格连接并组合成一个

MoveVerte

移动网格顶点

Ifibonacc

使用斐波那契数列的索引返回相应的数字或连续的对数字。

RndRange

在域内创建一系列随机值。

RatioBo

用作视觉参考的框以帮助按比例调整设计参数

逻辑叶轮机

以下是使用这些组件创建植物的基本步骤：

PhylloMesh（允许它的任何组件）生成词干或主要形式。
爆炸面。
选择面。根据功能划分面孔列表（例如：花瓣、叶子、其余部分）。
创建形状曲线。我们使用选定的面为花瓣或叶子创建曲线形状。
创建器官。我们从选定的面和它们的面制作花瓣、叶子和树枝形状曲线。
我们加入所有网格。花瓣、树叶和所有其他未使用的面。
平滑焊接网。最好使用 Weaverbird 的 Catmull-Clark Subdivision。在 ExampleFiles 文件夹中，您将找到几个示例和详细教程 (1DaisyTutorial)。

下次更新

我为那些想要继续发展的人留下了几条路可以走千叶机。任何人都可以自由分享新功能、进行改进或更改，只要满足许可条件。特别是我还没有解决的两个问题：

PhylloMesh 分支。将几条曲线同时包裹在一个 phyllomesh 中，这样我们就可以创建来自一系列相交曲线的相互连接的分支。类似于 ExoWireframe，但带有叶状体。
L 系统。为此，PhylloMachine 组件已被编码为一个类。你可以加插件的所有组件都作为此类的函数，并将它们与 L-System 一起使用。然后系统将使用它自己的语法（或使用通常的语法）来建模通过简单的规则处理。它应该是一个不同于经典的 L 系统，因为它不仅应该生成线条，还应该生成 phyllo-wrap 和植物的其他器官。

我鼓励任何对这种生成建模有经验的人感兴趣联系我。结果简直太棒了

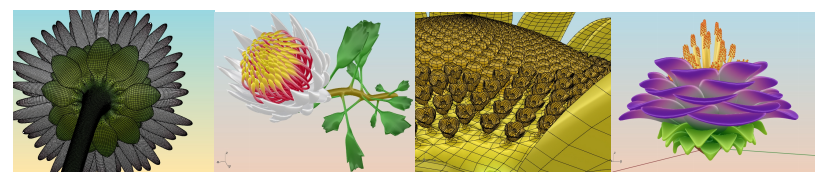
斐波那契数列原理解析与Grasshopper插件应用